Species Sensitivity Distribution (SSD) for endosulfan
endosulfan.RdSummary of 48- to 96-hour acute toxicity values (LC50 and EC50 values) for exposure of Australian an Non-Australian taxa to endosulfan.
Usage
data(endosulfan)Format
endosulfan is a data frame with 4 columns, named ATV for Acute Toxicity Value
(geometric mean of LC50 ou EC50 values in micrograms per liter),
Australian (coding for Australian or another origin), group
(arthropods, fish or non-arthropod invertebrates) and taxa.
Source
Hose, G.C., Van den Brink, P.J. 2004. Confirming the Species-Sensitivity Distribution Concept for Endosulfan Using Laboratory, Mesocosms, and Field Data. Archives of Environmental Contamination and Toxicology, 47, 511-520.
Examples
# (1) load of data
#
data(endosulfan)
# (2) plot and description of data for non Australian fish in decimal logarithm
#
log10ATV <-log10(subset(endosulfan,(Australian == "no") & (group == "Fish"))$ATV)
plotdist(log10ATV)
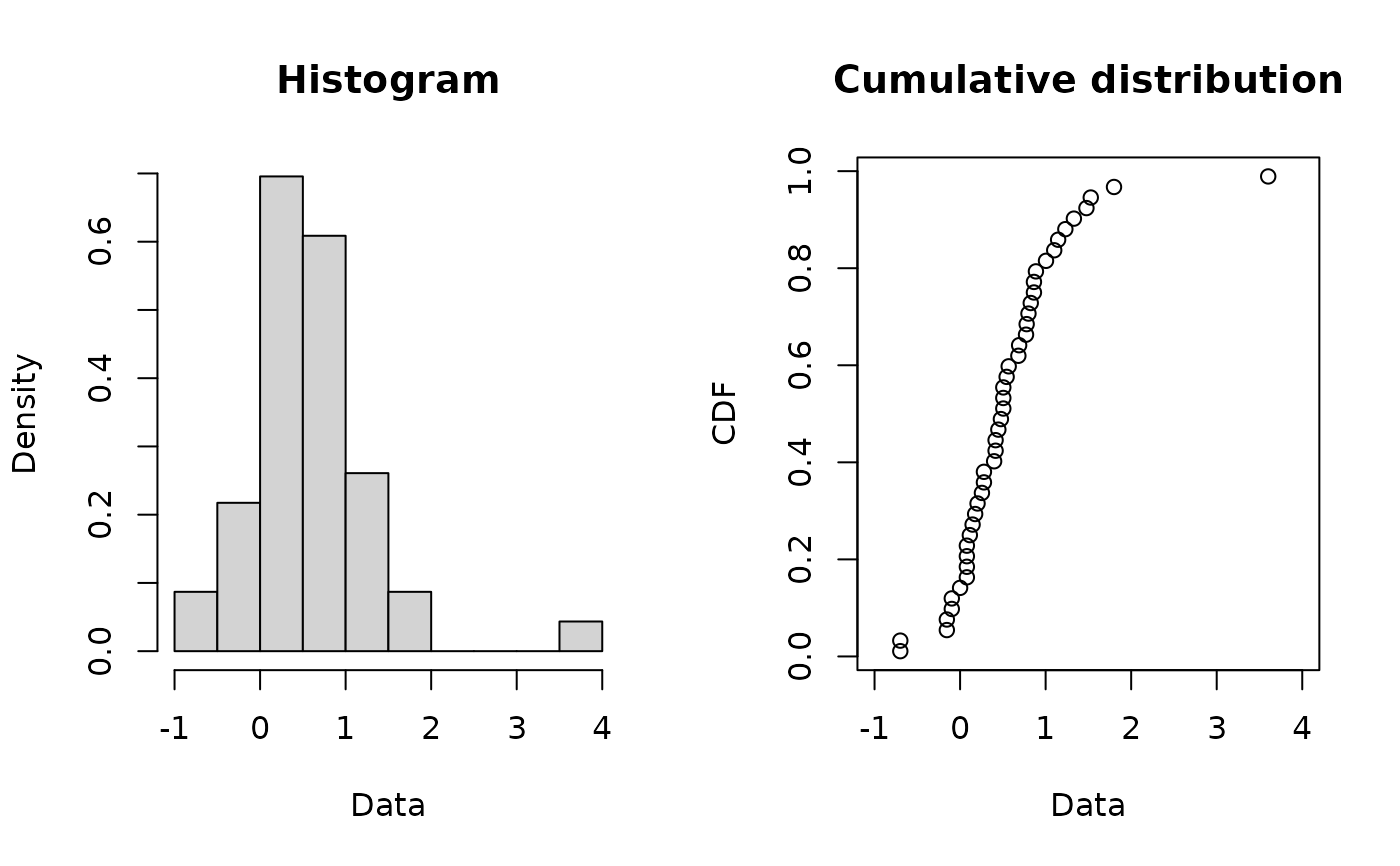 descdist(log10ATV,boot=11)
descdist(log10ATV,boot=11)
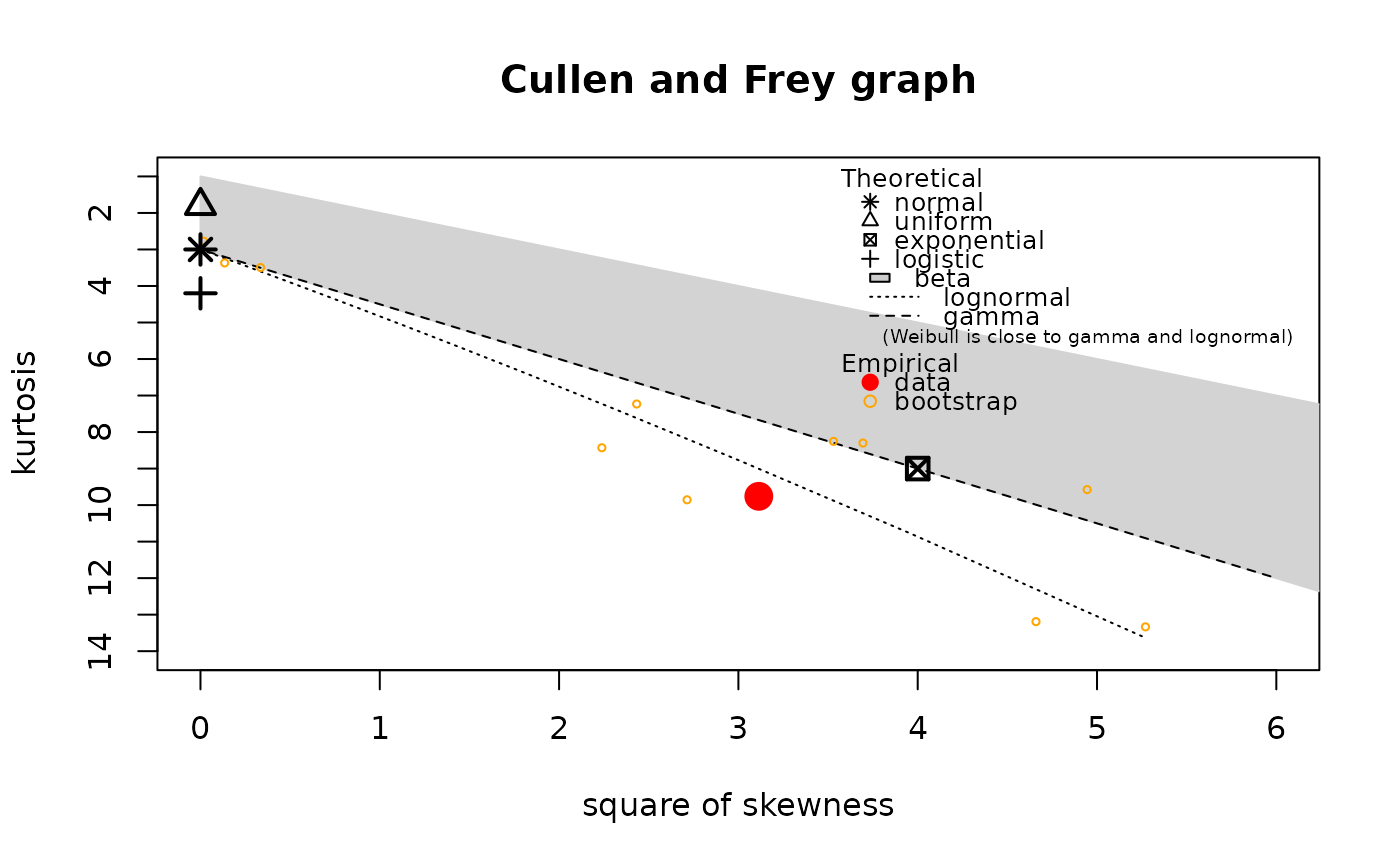 #> summary statistics
#> ------
#> min: -0.69897 max: 3.60206
#> median: 0.4911356
#> mean: 0.5657595
#> estimated sd: 0.7034928
#> estimated skewness: 1.764601
#> estimated kurtosis: 9.759505
# (3) fit of a normal and a logistic distribution to data in log10
# (classical distributions used for SSD)
# and visual comparison of the fits
#
fln <- fitdist(log10ATV,"norm")
summary(fln)
#> Fitting of the distribution ' norm ' by maximum likelihood
#> Parameters :
#> estimate Std. Error
#> mean 0.5657595 0.10259072
#> sd 0.6958041 0.07254192
#> Loglikelihood: -48.58757 AIC: 101.1751 BIC: 104.8324
#> Correlation matrix:
#> mean sd
#> mean 1 0
#> sd 0 1
#>
fll <- fitdist(log10ATV,"logis")
summary(fll)
#> Fitting of the distribution ' logis ' by maximum likelihood
#> Parameters :
#> estimate Std. Error
#> location 0.5082818 0.08701594
#> scale 0.3457256 0.04301025
#> Loglikelihood: -44.31825 AIC: 92.6365 BIC: 96.29378
#> Correlation matrix:
#> location scale
#> location 1.00000000 0.04028287
#> scale 0.04028287 1.00000000
#>
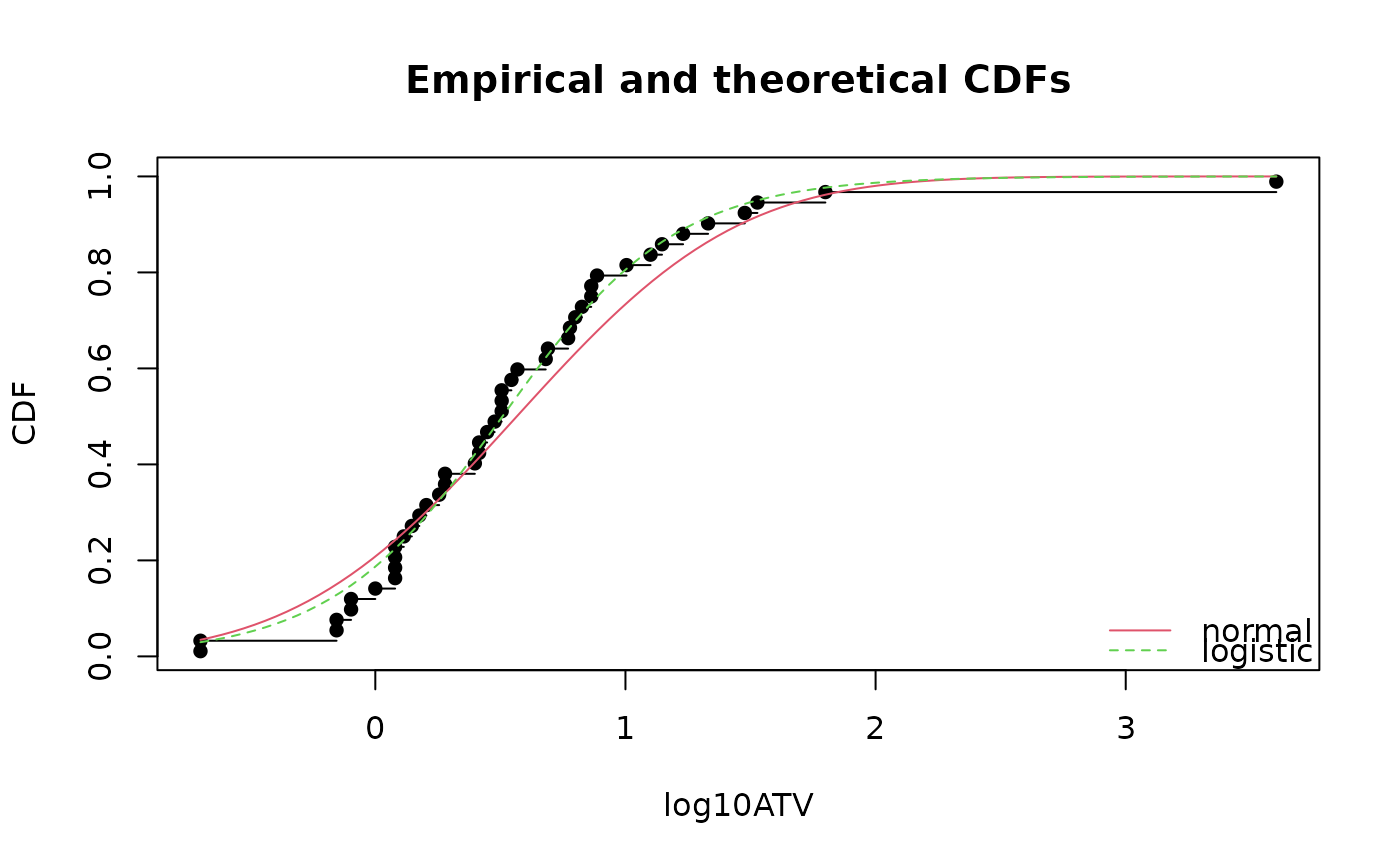
cdfcomp(list(fln,fll),legendtext=c("normal","logistic"),
xlab="log10ATV")
#> summary statistics
#> ------
#> min: -0.69897 max: 3.60206
#> median: 0.4911356
#> mean: 0.5657595
#> estimated sd: 0.7034928
#> estimated skewness: 1.764601
#> estimated kurtosis: 9.759505
# (3) fit of a normal and a logistic distribution to data in log10
# (classical distributions used for SSD)
# and visual comparison of the fits
#
fln <- fitdist(log10ATV,"norm")
summary(fln)
#> Fitting of the distribution ' norm ' by maximum likelihood
#> Parameters :
#> estimate Std. Error
#> mean 0.5657595 0.10259072
#> sd 0.6958041 0.07254192
#> Loglikelihood: -48.58757 AIC: 101.1751 BIC: 104.8324
#> Correlation matrix:
#> mean sd
#> mean 1 0
#> sd 0 1
#>
fll <- fitdist(log10ATV,"logis")
summary(fll)
#> Fitting of the distribution ' logis ' by maximum likelihood
#> Parameters :
#> estimate Std. Error
#> location 0.5082818 0.08701594
#> scale 0.3457256 0.04301025
#> Loglikelihood: -44.31825 AIC: 92.6365 BIC: 96.29378
#> Correlation matrix:
#> location scale
#> location 1.00000000 0.04028287
#> scale 0.04028287 1.00000000
#>
cdfcomp(list(fln,fll),legendtext=c("normal","logistic"),
xlab="log10ATV")
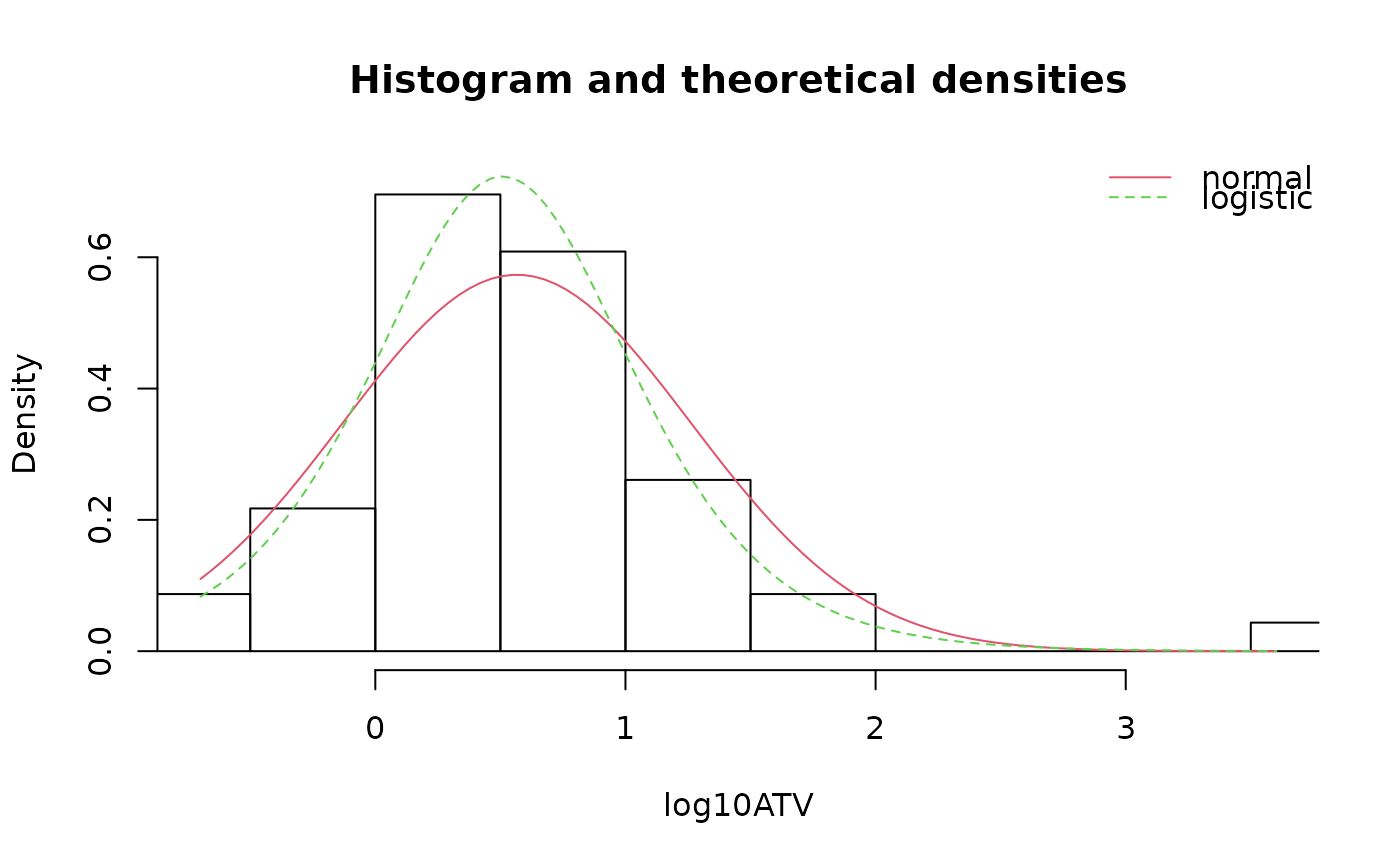
 denscomp(list(fln,fll),legendtext=c("normal","logistic"),
xlab="log10ATV")
denscomp(list(fln,fll),legendtext=c("normal","logistic"),
xlab="log10ATV")
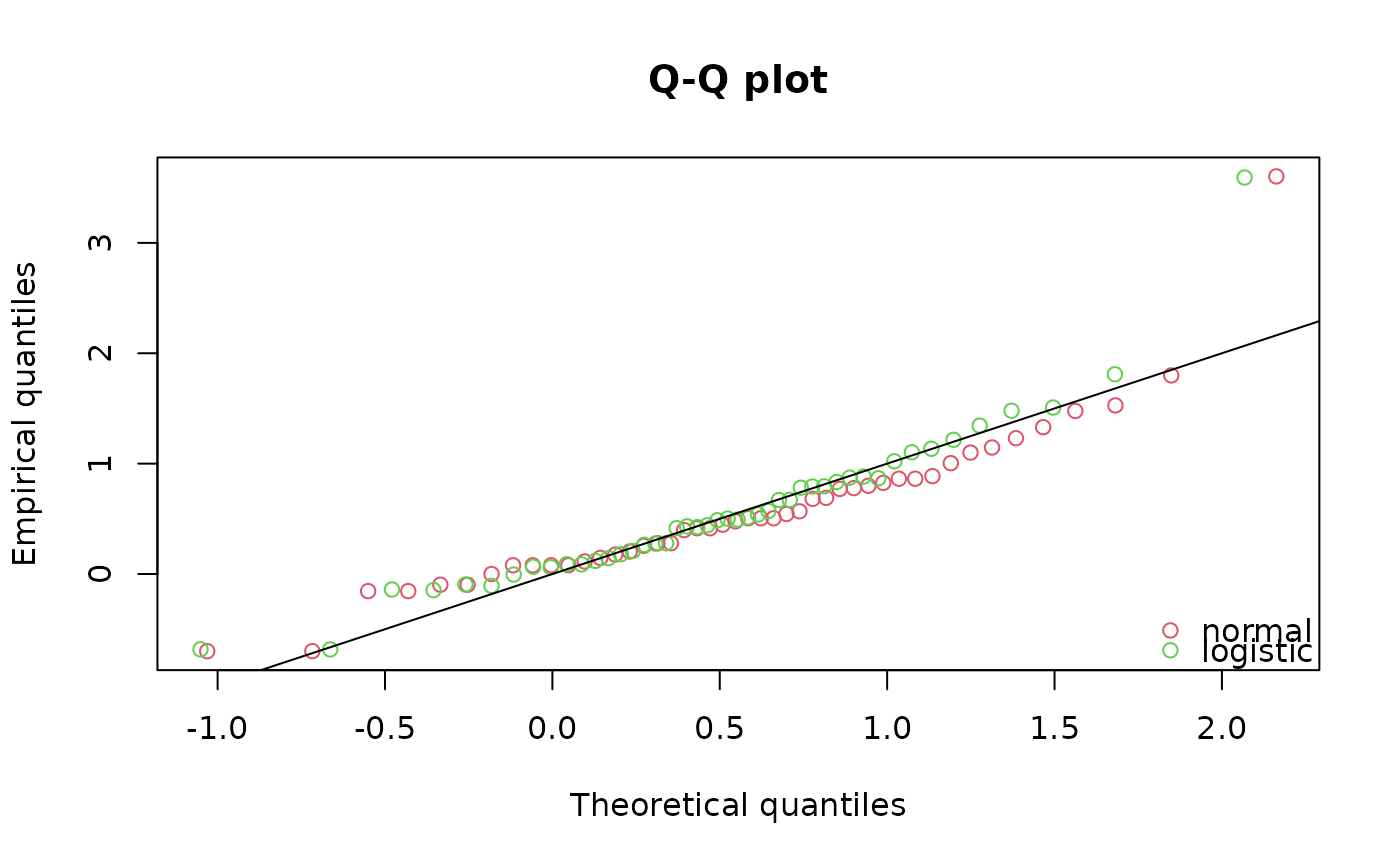
 qqcomp(list(fln,fll),legendtext=c("normal","logistic"))
qqcomp(list(fln,fll),legendtext=c("normal","logistic"))
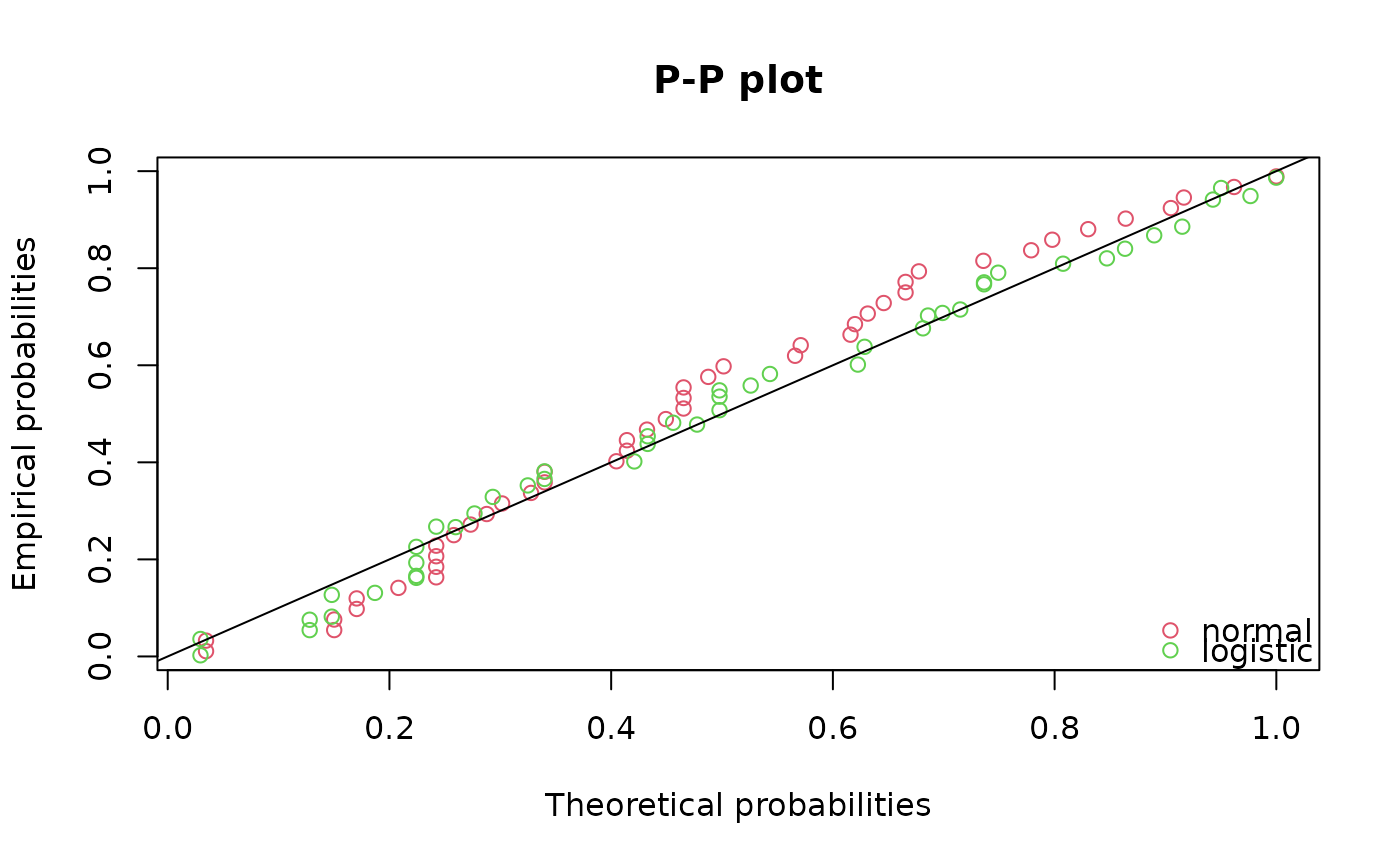
 ppcomp(list(fln,fll),legendtext=c("normal","logistic"))
ppcomp(list(fln,fll),legendtext=c("normal","logistic"))
 gofstat(list(fln,fll), fitnames = c("lognormal", "loglogistic"))
#> Goodness-of-fit statistics
#> lognormal loglogistic
#> Kolmogorov-Smirnov statistic 0.1267649 0.08457997
#> Cramer-von Mises statistic 0.1555576 0.04058514
#> Anderson-Darling statistic 1.0408045 0.37407465
#>
#> Goodness-of-fit criteria
#> lognormal loglogistic
#> Akaike's Information Criterion 101.1751 92.63650
#> Bayesian Information Criterion 104.8324 96.29378
# (4) estimation of the 5 percent quantile value of
# logistic fitted distribution (5 percent hazardous concentration : HC5)
# with its two-sided 95 percent confidence interval calculated by
# parametric bootstrap
# with a small number of iterations to satisfy CRAN running times constraint.
# For practical applications, we recommend to use at least niter=501 or niter=1001.
#
# in log10(ATV)
bll <- bootdist(fll,niter=51)
HC5ll <- quantile(bll,probs = 0.05)
# in ATV
10^(HC5ll$quantiles)
#> p=0.05
#> estimate 0.309253
10^(HC5ll$quantCI)
#> p=0.05
#> 2.5 % 0.1653427
#> 97.5 % 0.5676924
# (5) estimation of the 5 percent quantile value of
# the fitted logistic distribution (5 percent hazardous concentration : HC5)
# with its one-sided 95 percent confidence interval (type "greater")
# calculated by
# nonparametric bootstrap
# with a small number of iterations to satisfy CRAN running times constraint.
# For practical applications, we recommend to use at least niter=501 or niter=1001.
#
# in log10(ATV)
bllnonpar <- bootdist(fll,niter=51,bootmethod = "nonparam")
HC5llgreater <- quantile(bllnonpar,probs = 0.05, CI.type="greater")
# in ATV
10^(HC5llgreater$quantiles)
#> p=0.05
#> estimate 0.309253
10^(HC5llgreater$quantCI)
#> p=0.05
#> 5 % 0.1982323
# (6) fit of a logistic distribution
# by minimizing the modified Anderson-Darling AD2L distance
# cf. ?mgedist for definition of this distance
#
fllAD2L <- fitdist(log10ATV,"logis",method="mge",gof="AD2L")
summary(fllAD2L)
#> Fitting of the distribution ' logis ' by maximum goodness-of-fit
#> Parameters :
#> estimate
#> location 0.4965288
#> scale 0.3013154
#> Loglikelihood: -44.96884 AIC: 93.93767 BIC: 97.59496
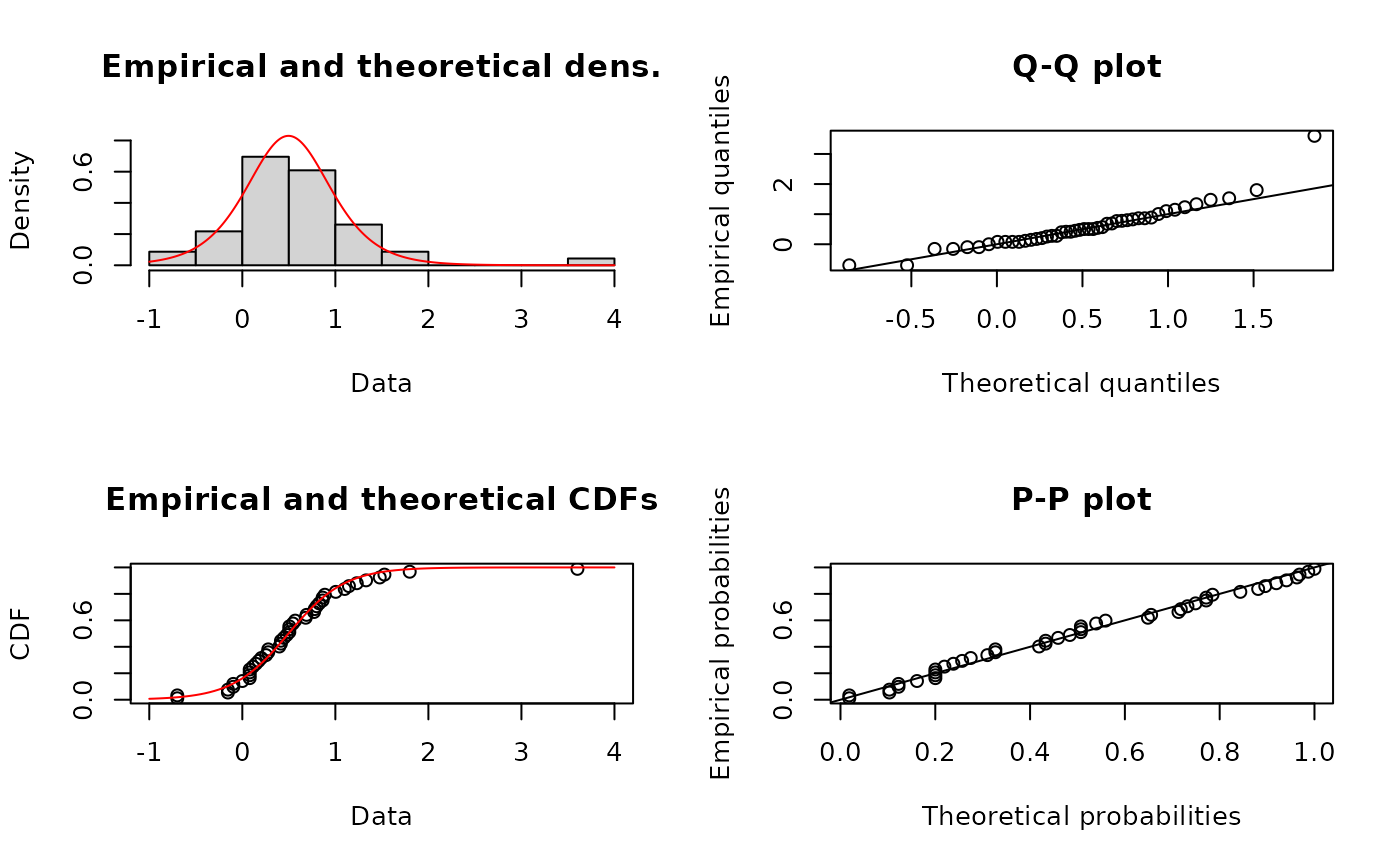
plot(fllAD2L)
gofstat(list(fln,fll), fitnames = c("lognormal", "loglogistic"))
#> Goodness-of-fit statistics
#> lognormal loglogistic
#> Kolmogorov-Smirnov statistic 0.1267649 0.08457997
#> Cramer-von Mises statistic 0.1555576 0.04058514
#> Anderson-Darling statistic 1.0408045 0.37407465
#>
#> Goodness-of-fit criteria
#> lognormal loglogistic
#> Akaike's Information Criterion 101.1751 92.63650
#> Bayesian Information Criterion 104.8324 96.29378
# (4) estimation of the 5 percent quantile value of
# logistic fitted distribution (5 percent hazardous concentration : HC5)
# with its two-sided 95 percent confidence interval calculated by
# parametric bootstrap
# with a small number of iterations to satisfy CRAN running times constraint.
# For practical applications, we recommend to use at least niter=501 or niter=1001.
#
# in log10(ATV)
bll <- bootdist(fll,niter=51)
HC5ll <- quantile(bll,probs = 0.05)
# in ATV
10^(HC5ll$quantiles)
#> p=0.05
#> estimate 0.309253
10^(HC5ll$quantCI)
#> p=0.05
#> 2.5 % 0.1653427
#> 97.5 % 0.5676924
# (5) estimation of the 5 percent quantile value of
# the fitted logistic distribution (5 percent hazardous concentration : HC5)
# with its one-sided 95 percent confidence interval (type "greater")
# calculated by
# nonparametric bootstrap
# with a small number of iterations to satisfy CRAN running times constraint.
# For practical applications, we recommend to use at least niter=501 or niter=1001.
#
# in log10(ATV)
bllnonpar <- bootdist(fll,niter=51,bootmethod = "nonparam")
HC5llgreater <- quantile(bllnonpar,probs = 0.05, CI.type="greater")
# in ATV
10^(HC5llgreater$quantiles)
#> p=0.05
#> estimate 0.309253
10^(HC5llgreater$quantCI)
#> p=0.05
#> 5 % 0.1982323
# (6) fit of a logistic distribution
# by minimizing the modified Anderson-Darling AD2L distance
# cf. ?mgedist for definition of this distance
#
fllAD2L <- fitdist(log10ATV,"logis",method="mge",gof="AD2L")
summary(fllAD2L)
#> Fitting of the distribution ' logis ' by maximum goodness-of-fit
#> Parameters :
#> estimate
#> location 0.4965288
#> scale 0.3013154
#> Loglikelihood: -44.96884 AIC: 93.93767 BIC: 97.59496
plot(fllAD2L)