Skip to contents

Which optimization algorithm to choose?

Marie Laure Delignette Muller, Christophe Dutang

2024-09-09

Source: vignettes/Optimalgo.Rmd
Optimalgo.Rmd

1 Quick overview of main optimization methods

We present very quickly the main optimization methods. Please refer to Numerical Optimization (Nocedal & Wright, 2006) or Numerical Optimization: theoretical and practical aspects (Bonnans, Gilbert, Lemarechal & Sagastizabal, 2006) for a good introduction. We consider the following problem \(\min_x f(x)\) for \(x\in\mathbb{R}^n\).

1.1 Derivative-free optimization methods

The Nelder-Mead method is one of the most well known derivative-free methods that use only values of \(f\) to search for the minimum. It consists in building a simplex of \(n+1\) points and moving/shrinking this simplex into the good direction.

  1. set initial points \(x_1, \dots, x_{n+1}\).
  2. order points such that \(f(x_1)\leq f(x_2)\leq\dots\leq f(x_{n+1})\).
  3. compute \(x_o\) as the centroid of \(x_1, \dots, x_{n}\).
  4. Reflection:
    • compute the reflected point \(x_r = x_o + \alpha(x_o-x_{n+1})\).
    • if \(f(x_1)\leq f(x_r)<f(x_n)\), then replace \(x_{n+1}\) by \(x_r\), go to step 2.
    • else go step 5.
  5. Expansion:
    • if \(f(x_r)<f(x_1)\), then compute the expansion point \(x_e= x_o+\gamma(x_o-x_{n+1})\).
    • if \(f(x_e) <f(x_r)\), then replace \(x_{n+1}\) by \(x_e\), go to step 2.
    • else \(x_{n+1}\) by \(x_r\), go to step 2.
    • else go to step 6.
  6. Contraction:
    • compute the contracted point \(x_c = x_o + \beta(x_o-x_{n+1})\).
    • if \(f(x_c)<f(x_{n+1})\), then replace \(x_{n+1}\) by \(x_c\), go to step 2.
    • else go step 7.
  7. Reduction:
    • for \(i=2,\dots, n+1\), compute \(x_i = x_1+\sigma(x_i-x_{1})\).

The Nelder-Mead method is available in optim. By default, in optim, \(\alpha=1\), \(\beta=1/2\), \(\gamma=2\) and \(\sigma=1/2\).

1.2 Hessian-free optimization methods

For smooth non-linear function, the following method is generally used: a local method combined with line search work on the scheme \(x_{k+1} =x_k + t_k d_{k}\), where the local method will specify the direction \(d_k\) and the line search will specify the step size \(t_k \in \mathbb{R}\).

1.2.1 Computing the direction \(d_k\)

A desirable property for \(d_k\) is that \(d_k\) ensures a descent \(f(x_{k+1}) < f(x_{k})\). Newton methods are such that \(d_k\) minimizes a local quadratic approximation of \(f\) based on a Taylor expansion, that is \(q_f(d) = f(x_k) + g(x_k)^Td +\frac{1}{2} d^T H(x_k) d\) where \(g\) denotes the gradient and \(H\) denotes the Hessian.

The consists in using the exact solution of local minimization problem \(d_k = - H(x_k)^{-1} g(x_k)\).
In practice, other methods are preferred (at least to ensure positive definiteness). The method approximates the Hessian by a matrix \(H_k\) as a function of \(H_{k-1}\), \(x_k\), \(f(x_k)\) and then \(d_k\) solves the system \(H_k d = - g(x_k)\). Some implementation may also directly approximate the inverse of the Hessian \(W_k\) in order to compute \(d_k = -W_k g(x_k)\). Using the Sherman-Morrison-Woodbury formula, we can switch between \(W_k\) and \(H_k\).

To determine \(W_k\), first it must verify the secant equation \(H_k y_k =s_k\) or \(y_k=W_k s_k\) where \(y_k = g_{k+1}-g_k\) and \(s_k=x_{k+1}-x_k\). To define the \(n(n-1)\) terms, we generally impose a symmetry and a minimum distance conditions. We say we have a rank 2 update if \(H_k = H_{k-1} + a u u^T + b v v^T\) and a rank 1 update if $H_k = H_{k-1} + a u u^T $. Rank \(n\) update is justified by the spectral decomposition theorem.

There are two rank-2 updates which are symmetric and preserve positive definiteness

  • DFP minimizes \(\min || H - H_k ||_F\) such that \(H=H^T\): \[ H_{k+1} = \left (I-\frac {y_k s_k^T} {y_k^T s_k} \right ) H_k \left (I-\frac {s_k y_k^T} {y_k^T s_k} \right )+\frac{y_k y_k^T} {y_k^T s_k} \Leftrightarrow W_{k+1} = W_k + \frac{s_k s_k^T}{y_k^{T} s_k} - \frac {W_k y_k y_k^T W_k^T} {y_k^T W_k y_k} . \]
  • BFGS minimizes \(\min || W - W_k ||_F\) such that \(W=W^T\): \[ H_{k+1} = H_k - \frac{ H_k y_k y_k^T H_k }{ y_k^T H_k y_k } + \frac{ s_k s_k^T }{ y_k^T s_k } \Leftrightarrow W_{k+1} = \left (I-\frac {y_k s_k^T} {y_k^T s_k} \right )^T W_k \left (I-\frac { y_k s_k^T} {y_k^T s_k} \right )+\frac{s_k s_k^T} {y_k^T s_k} . \]

In R, the so-called BFGS scheme is implemented in optim.

Another possible method (which is initially arised from quadratic problems) is the nonlinear conjugate gradients. This consists in computing directions \((d_0, \dots, d_k)\) that are conjugate with respect to a matrix close to the true Hessian \(H(x_k)\). Directions are computed iteratively by \(d_k = -g(x_k) + \beta_k d_{k-1}\) for \(k>1\), once initiated by \(d_1 = -g(x_1)\). \(\beta_k\) are updated according a scheme:

  • \(\beta_k = \frac{ g_k^T g_k}{g_{k-1}^T g_{k-1} }\): Fletcher-Reeves update,
  • \(\beta_k = \frac{ g_k^T (g_k-g_{k-1} )}{g_{k-1}^T g_{k-1}}\): Polak-Ribiere update.

There exists also three-term formula for computing direction \(d_k = -g(x_k) + \beta_k d_{k-1}+\gamma_{k} d_t\) for \(t<k\). A possible scheme is the Beale-Sorenson update defined as \(\beta_k = \frac{ g_k^T (g_k-g_{k-1} )}{d^T_{k-1}(g_{k}- g_{k-1})}\) and \(\gamma_k = \frac{ g_k^T (g_{t+1}-g_{t} )}{d^T_{t}(g_{t+1}- g_{t})}\) if \(k>t+1\) otherwise \(\gamma_k=0\) if \(k=t\). See Yuan (2006) for other well-known schemes such as Hestenses-Stiefel, Dixon or Conjugate-Descent. The three updates (Fletcher-Reeves, Polak-Ribiere, Beale-Sorenson) of the (non-linear) conjugate gradient are available in optim.

1.2.2 Computing the stepsize \(t_k\)

Let \(\phi_k(t) = f(x_k + t d_k)\) for a given direction/iterate \((d_k, x_k)\). We need to find conditions to find a satisfactory stepsize \(t_k\). In literature, we consider the descent condition: \(\phi_k'(0) < 0\) and the Armijo condition: \(\phi_k(t) \leq \phi_k(0) + t c_1 \phi_k'(0)\) ensures a decrease of \(f\). Nocedal & Wright (2006) presents a backtracking (or geometric) approach satisfying the Armijo condition and minimal condition, i.e. Goldstein and Price condition.

  • set \(t_{k,0}\) e.g. 1, \(0 < \alpha < 1\),
  • Repeat until Armijo satisfied,
    • \(t_{k,i+1} = \alpha \times t_{k,i}\).
  • end Repeat

This backtracking linesearch is available in optim.

1.3 Benchmark

To simplify the benchmark of optimization methods, we create a fitbench function that computes the desired estimation method for all optimization methods. This function is currently not exported in the package.

fitbench <- function(data, distr, method, grad = NULL, 
                     control = list(trace = 0, REPORT = 1, maxit = 1000), 
                     lower = -Inf, upper = +Inf, ...)

2 Numerical illustration with the beta distribution

2.1 Log-likelihood function and its gradient for beta distribution

2.1.1 Theoretical value

The density of the beta distribution is given by \[ f(x; \delta_1,\delta_2) = \frac{x^{\delta_1-1}(1-x)^{\delta_2-1}}{\beta(\delta_1,\delta_2)}, \] where \(\beta\) denotes the beta function, see the NIST Handbook of mathematical functions https://dlmf.nist.gov/. We recall that \(\beta(a,b)=\Gamma(a)\Gamma(b)/\Gamma(a+b)\). There the log-likelihood for a set of observations \((x_1,\dots,x_n)\) is \[ \log L(\delta_1,\delta_2) = (\delta_1-1)\sum_{i=1}^n\log(x_i)+ (\delta_2-1)\sum_{i=1}^n\log(1-x_i)+ n \log(\beta(\delta_1,\delta_2)) \] The gradient with respect to \(a\) and \(b\) is \[ \nabla \log L(\delta_1,\delta_2) = \left(\begin{matrix} \sum\limits_{i=1}^n\ln(x_i) - n\psi(\delta_1)+n\psi( \delta_1+\delta_2) \\ \sum\limits_{i=1}^n\ln(1-x_i)- n\psi(\delta_2)+n\psi( \delta_1+\delta_2) \end{matrix}\right), \] where \(\psi(x)=\Gamma'(x)/\Gamma(x)\) is the digamma function, see the NIST Handbook of mathematical functions https://dlmf.nist.gov/.

2.1.2 R implementation

As in the fitdistrplus package, we minimize the opposite of the log-likelihood: we implement the opposite of the gradient in grlnL. Both the log-likelihood and its gradient are not exported.

lnL <- function(par, fix.arg, obs, ddistnam) 
  fitdistrplus:::loglikelihood(par, fix.arg, obs, ddistnam) 
grlnlbeta <- fitdistrplus:::grlnlbeta

2.2 Random generation of a sample 

#(1) beta distribution
n <- 200
x <- rbeta(n, 3, 3/4)
grlnlbeta(c(3, 4), x) #test
## [1] -133  317
hist(x, prob=TRUE, xlim=0:1)
lines(density(x), col="red")
curve(dbeta(x, 3, 3/4), col="green", add=TRUE)
legend("topleft", lty=1, col=c("red","green"), legend=c("empirical", "theoretical"), bty="n")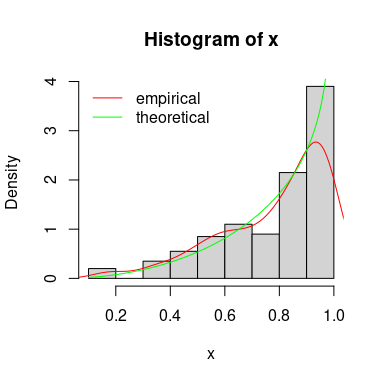

2.3 Fit Beta distribution

Define control parameters.

ctr <- list(trace=0, REPORT=1, maxit=1000)

Call mledist with the default optimization function (optim implemented in stats package) with and without the gradient for the different optimization methods.

unconstropt <- fitbench(x, "beta", "mle", grad=grlnlbeta, lower=0)
##     BFGS       NM     CGFR     CGPR     CGBS L-BFGS-B     NM-B   G-BFGS 
##       14       14       14       14       14       14       14       14 
##   G-CGFR   G-CGPR   G-CGBS G-BFGS-B   G-NM-B G-CGFR-B G-CGPR-B G-CGBS-B 
##       14       14       14       14       14       14       14       14

In the case of constrained optimization, mledist permits the direct use of constrOptim function (still implemented in stats package) that allow linear inequality constraints by using a logarithmic barrier.

Use a exp/log transformation of the shape parameters \(\delta_1\) and \(\delta_2\) to ensure that the shape parameters are strictly positive.

dbeta2 <- function(x, shape1, shape2, log)
  dbeta(x, exp(shape1), exp(shape2), log=log)
#take the log of the starting values
startarg <- lapply(fitdistrplus:::startargdefault(x, "beta"), log)
#redefine the gradient for the new parametrization
grbetaexp <- function(par, obs, ...) 
    grlnlbeta(exp(par), obs) * exp(par)
    

expopt <- fitbench(x, distr="beta2", method="mle", grad=grbetaexp, start=startarg) 
##   BFGS     NM   CGFR   CGPR   CGBS G-BFGS G-CGFR G-CGPR G-CGBS 
##     14     14     14     14     14     14     14     14     14
#get back to original parametrization
expopt[c("fitted shape1", "fitted shape2"), ] <- exp(expopt[c("fitted shape1", "fitted shape2"), ])

Then we extract the values of the fitted parameters, the value of the corresponding log-likelihood and the number of counts to the function to minimize and its gradient (whether it is the theoretical gradient or the numerically approximated one).

2.4 Results of the numerical investigation

Results are displayed in the following tables: (1) the original parametrization without specifying the gradient (-B stands for bounded version), (2) the original parametrization with the (true) gradient (-B stands for bounded version and -G for gradient), (3) the log-transformed parametrization without specifying the gradient, (4) the log-transformed parametrization with the (true) gradient (-G stands for gradient).

Table 2.1: Unconstrained optimization with approximated gradient
BFGS NM CGFR CGPR CGBS L-BFGS-B NM-B
fitted shape1 2.665 2.664 2.665 2.665 2.665 2.665 2.665
fitted shape2 0.731 0.731 0.731 0.731 0.731 0.731 0.731
fitted loglik 114.165 114.165 114.165 114.165 114.165 114.165 114.165
func. eval. nb. 23.000 47.000 211.000 263.000 183.000 11.000 47.000
grad. eval. nb. 5.000 NA 53.000 69.000 47.000 11.000 NA
time (sec) 0.005 0.004 0.023 0.028 0.020 0.004 0.008
Table 2.2: Unconstrained optimization with true gradient
G-BFGS G-CGFR G-CGPR G-CGBS G-BFGS-B G-NM-B G-CGFR-B G-CGPR-B G-CGBS-B
fitted shape1 2.665 2.665 2.665 2.665 2.665 2.665 2.665 2.665 2.665
fitted shape2 0.731 0.731 0.731 0.731 0.731 0.731 0.731 0.731 0.731
fitted loglik 114.165 114.165 114.165 114.165 114.165 114.165 114.165 114.165 114.165
func. eval. nb. 20.000 249.000 225.000 138.000 25.000 47.000 263.000 188.000 176.000
grad. eval. nb. 5.000 71.000 69.000 43.000 5.000 NA 69.000 59.000 47.000
time (sec) 0.010 0.075 0.072 0.046 0.014 0.013 0.087 0.077 0.065
Table 2.3: Exponential trick optimization with approximated gradient
BFGS NM CGFR CGPR CGBS
fitted shape1 2.665 2.664 2.665 2.665 2.665
fitted shape2 0.731 0.731 0.731 0.731 0.731
fitted loglik 114.165 114.165 114.165 114.165 114.165
func. eval. nb. 18.000 41.000 131.000 116.000 134.000
grad. eval. nb. 5.000 NA 27.000 29.000 35.000
time (sec) 0.015 0.003 0.014 0.013 0.015
Table 2.4: Exponential trick optimization with true gradient
G-BFGS G-CGFR G-CGPR G-CGBS
fitted shape1 2.665 2.665 2.665 2.665
fitted shape2 0.731 0.731 0.731 0.731
fitted loglik 114.165 114.165 114.165 114.165
func. eval. nb. 20.000 175.000 125.000 112.000
grad. eval. nb. 5.000 39.000 41.000 35.000
time (sec) 0.011 0.044 0.043 0.038

Using llsurface, we plot the log-likehood surface around the true value (green) and the fitted parameters (red).

llsurface(min.arg=c(0.1, 0.1), max.arg=c(7, 3), xlim=c(.1,7), 
          plot.arg=c("shape1", "shape2"), nlev=25,
          lseq=50, data=x, distr="beta", back.col = FALSE)
points(unconstropt[1,"BFGS"], unconstropt[2,"BFGS"], pch="+", col="red")
points(3, 3/4, pch="x", col="green")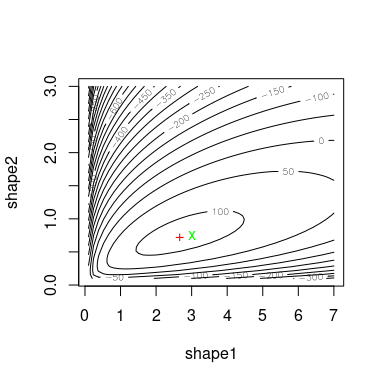

We can simulate bootstrap replicates using the bootdist function.

b1 <- bootdist(fitdist(x, "beta", method = "mle", optim.method = "BFGS"), 
               niter = 100, parallel = "snow", ncpus = 2)
summary(b1)
## Parametric bootstrap medians and 95% percentile CI 
##        Median  2.5% 97.5%
## shape1   2.73 2.272 3.283
## shape2   0.75 0.652 0.888
plot(b1, trueval = c(3, 3/4))

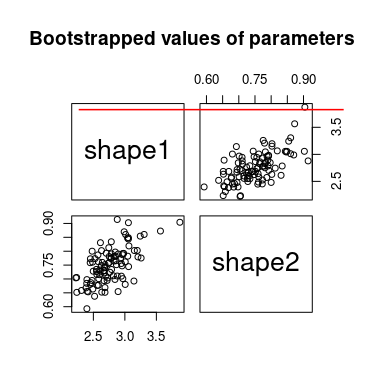
3 Numerical illustration with the negative binomial distribution

3.1 Log-likelihood function and its gradient for negative binomial distribution

3.1.1 Theoretical value

The p.m.f. of the Negative binomial distribution is given by \[ f(x; m,p) = \frac{\Gamma(x+m)}{\Gamma(m)x!} p^m (1-p)^x, \] where \(\Gamma\) denotes the beta function, see the NIST Handbook of mathematical functions https://dlmf.nist.gov/. There exists an alternative representation where \(\mu=m (1-p)/p\) or equivalently \(p=m/(m+\mu)\). Thus, the log-likelihood for a set of observations \((x_1,\dots,x_n)\) is \[ \log L(m,p) = \sum_{i=1}^{n} \log\Gamma(x_i+m) -n\log\Gamma(m) -\sum_{i=1}^{n} \log(x_i!) + mn\log(p) +\sum_{i=1}^{n} {x_i}\log(1-p) \] The gradient with respect to \(m\) and \(p\) is \[ \nabla \log L(m,p) = \left(\begin{matrix} \sum_{i=1}^{n} \psi(x_i+m) -n \psi(m) + n\log(p) \\ mn/p -\sum_{i=1}^{n} {x_i}/(1-p) \end{matrix}\right), \] where \(\psi(x)=\Gamma'(x)/\Gamma(x)\) is the digamma function, see the NIST Handbook of mathematical functions https://dlmf.nist.gov/.

3.1.2 R implementation

As in the fitdistrplus package, we minimize the opposite of the log-likelihood: we implement the opposite of the gradient in grlnL.

grlnlNB <- function(x, obs, ...)
{
  m <- x[1]
  p <- x[2]
  n <- length(obs)
  c(sum(psigamma(obs+m)) - n*psigamma(m) + n*log(p),
    m*n/p - sum(obs)/(1-p))
}

3.2 Random generation of a sample 

#(2) negative binomial distribution
n <- 200
trueval <- c("size"=10, "prob"=3/4, "mu"=10/3)
x <- rnbinom(n, trueval["size"], trueval["prob"])

hist(x, prob=TRUE, ylim=c(0, .3), xlim=c(0, 10))
lines(density(x), col="red")
points(min(x):max(x), dnbinom(min(x):max(x), trueval["size"], trueval["prob"]), 
       col = "green")
legend("topright", lty = 1, col = c("red", "green"), 
       legend = c("empirical", "theoretical"), bty="n")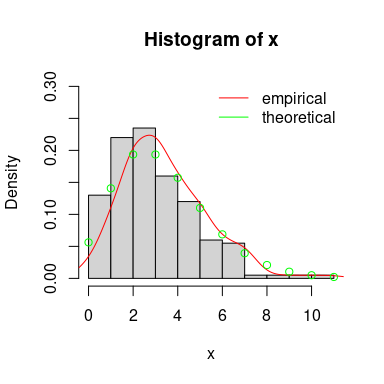

3.3 Fit a negative binomial distribution

Define control parameters and make the benchmark.

ctr <- list(trace = 0, REPORT = 1, maxit = 1000)
unconstropt <- fitbench(x, "nbinom", "mle", grad = grlnlNB, lower = 0)
##     BFGS       NM     CGFR     CGPR     CGBS L-BFGS-B     NM-B   G-BFGS 
##       14       14       14       14       14       14       14       14 
##   G-CGFR   G-CGPR   G-CGBS G-BFGS-B   G-NM-B G-CGFR-B G-CGPR-B G-CGBS-B 
##       14       14       14       14       14       14       14       14
unconstropt <- rbind(unconstropt, 
                     "fitted prob" = unconstropt["fitted mu", ] / (1 + unconstropt["fitted mu", ]))

In the case of constrained optimization, mledist permits the direct use of constrOptim function (still implemented in stats package) that allow linear inequality constraints by using a logarithmic barrier.

Use a exp/log transformation of the shape parameters \(\delta_1\) and \(\delta_2\) to ensure that the shape parameters are strictly positive.

dnbinom2 <- function(x, size, prob, log)
  dnbinom(x, exp(size), 1 / (1 + exp(-prob)), log = log)
# transform starting values
startarg <- fitdistrplus:::startargdefault(x, "nbinom")
startarg$mu <- startarg$size / (startarg$size + startarg$mu)
startarg <- list(size = log(startarg[[1]]), 
                 prob = log(startarg[[2]] / (1 - startarg[[2]])))

# redefine the gradient for the new parametrization
Trans <- function(x)
  c(exp(x[1]), plogis(x[2]))
grNBexp <- function(par, obs, ...) 
    grlnlNB(Trans(par), obs) * c(exp(par[1]), plogis(x[2])*(1-plogis(x[2])))

expopt <- fitbench(x, distr="nbinom2", method="mle", grad=grNBexp, start=startarg) 
##   BFGS     NM   CGFR   CGPR   CGBS G-BFGS G-CGFR G-CGPR G-CGBS 
##     14     14     14     14     14     14     14     14     14
# get back to original parametrization
expopt[c("fitted size", "fitted prob"), ] <- 
  apply(expopt[c("fitted size", "fitted prob"), ], 2, Trans)

Then we extract the values of the fitted parameters, the value of the corresponding log-likelihood and the number of counts to the function to minimize and its gradient (whether it is the theoretical gradient or the numerically approximated one).

3.4 Results of the numerical investigation

Results are displayed in the following tables: (1) the original parametrization without specifying the gradient (-B stands for bounded version), (2) the original parametrization with the (true) gradient (-B stands for bounded version and -G for gradient), (3) the log-transformed parametrization without specifying the gradient, (4) the log-transformed parametrization with the (true) gradient (-G stands for gradient).

Table 3.1: Unconstrained optimization with approximated gradient
BFGS NM CGFR CGPR CGBS L-BFGS-B NM-B
fitted size 61.944 68.138 61.969 62.364 62.878 61.944 67.397
fitted mu 3.425 3.425 3.425 3.425 3.425 3.425 3.425
fitted loglik -401.612 -401.611 -401.612 -401.612 -401.612 -401.612 -401.611
func. eval. nb. 2.000 37.000 2999.000 2680.000 2610.000 2.000 0.000
grad. eval. nb. 1.000 NA 1001.000 1001.000 1001.000 2.000 NA
time (sec) 0.002 0.002 0.222 0.207 0.206 0.001 0.002
fitted prob 0.774 0.774 0.774 0.774 0.774 0.774 0.774
Table 3.2: Unconstrained optimization with true gradient
G-BFGS G-CGFR G-CGPR G-CGBS G-BFGS-B G-NM-B G-CGFR-B G-CGPR-B G-CGBS-B
fitted size 61.944 61.944 61.944 61.944 61.944 67.397 61.944 61.944 61.944
fitted mu 3.425 3.425 3.425 3.425 3.425 3.425 3.425 3.425 3.425
fitted loglik -401.612 -401.612 -401.612 -401.612 -401.612 -401.611 -401.612 -401.612 -401.612
func. eval. nb. 26.000 881.000 174.000 881.000 0.000 0.000 0.000 0.000 0.000
grad. eval. nb. 1.000 59.000 11.000 59.000 NA NA NA NA NA
time (sec) 0.008 0.032 0.007 0.032 0.002 0.002 0.032 0.007 0.031
fitted prob 0.774 0.774 0.774 0.774 0.774 0.774 0.774 0.774 0.774
Table 3.3: Exponential trick optimization with approximated gradient
BFGS NM CGFR CGPR CGBS
fitted size 61.946 67.787 63.450 67.941 67.884
fitted prob 0.948 0.952 0.949 0.952 0.952
fitted loglik -401.612 -401.611 -401.612 -401.611 -401.611
func. eval. nb. 6.000 47.000 4001.000 3721.000 381.000
grad. eval. nb. 1.000 NA 1001.000 1001.000 97.000
time (sec) 0.004 0.002 0.258 0.235 0.024
Table 3.4: Exponential trick optimization with true gradient
G-BFGS G-CGFR G-CGPR G-CGBS
fitted size 61.944 61.944 61.944 61.944
fitted prob 0.948 0.948 0.948 0.948
fitted loglik -401.612 -401.612 -401.612 -401.612
func. eval. nb. 21.000 43.000 42.000 42.000
grad. eval. nb. 1.000 3.000 3.000 3.000
time (sec) 0.007 0.002 0.002 0.002

Using llsurface, we plot the log-likehood surface around the true value (green) and the fitted parameters (red).

llsurface(min.arg = c(5, 0.3), max.arg = c(15, 1), xlim=c(5, 15),
          plot.arg = c("size", "prob"), nlev = 25,
          lseq = 50, data = x, distr = "nbinom", back.col = FALSE)
points(unconstropt["fitted size", "BFGS"], unconstropt["fitted prob", "BFGS"], 
       pch = "+", col = "red")
points(trueval["size"], trueval["prob"], pch = "x", col = "green")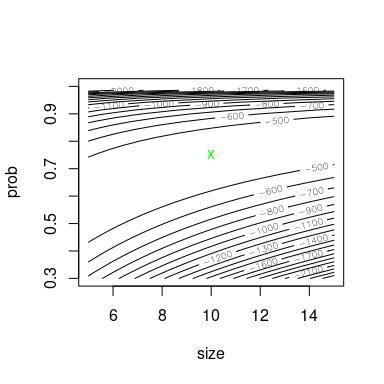

We can simulate bootstrap replicates using the bootdist function.

b1 <- bootdist(fitdist(x, "nbinom", method = "mle", optim.method = "BFGS"), 
               niter = 100, parallel = "snow", ncpus = 2)
summary(b1)
## Parametric bootstrap medians and 95% percentile CI 
##      Median  2.5%  97.5%
## size  61.95 11.05 118.32
## mu     3.43  3.17   3.72
## 
## The estimation method converged only for 76 among 100 iterations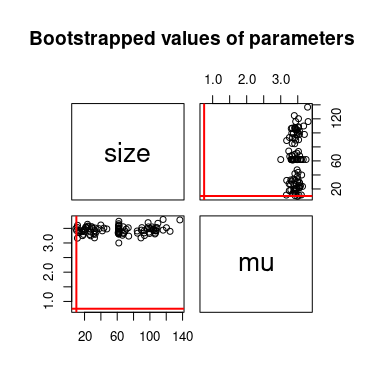
plot(b1, trueval=trueval[c("size", "mu")])

4 Conclusion

Based on the two previous examples, we observe that all methods converge to the same point. This is reassuring.
However, the number of function evaluations (and the gradient evaluations) is very different from a method to another. Furthermore, specifying the true gradient of the log-likelihood does not help at all the fitting procedure and generally slows down the convergence. Generally, the best method is the standard BFGS method or the BFGS method with the exponential transformation of the parameters. Since the exponential function is differentiable, the asymptotic properties are still preserved (by the Delta method) but for finite-sample this may produce a small bias.