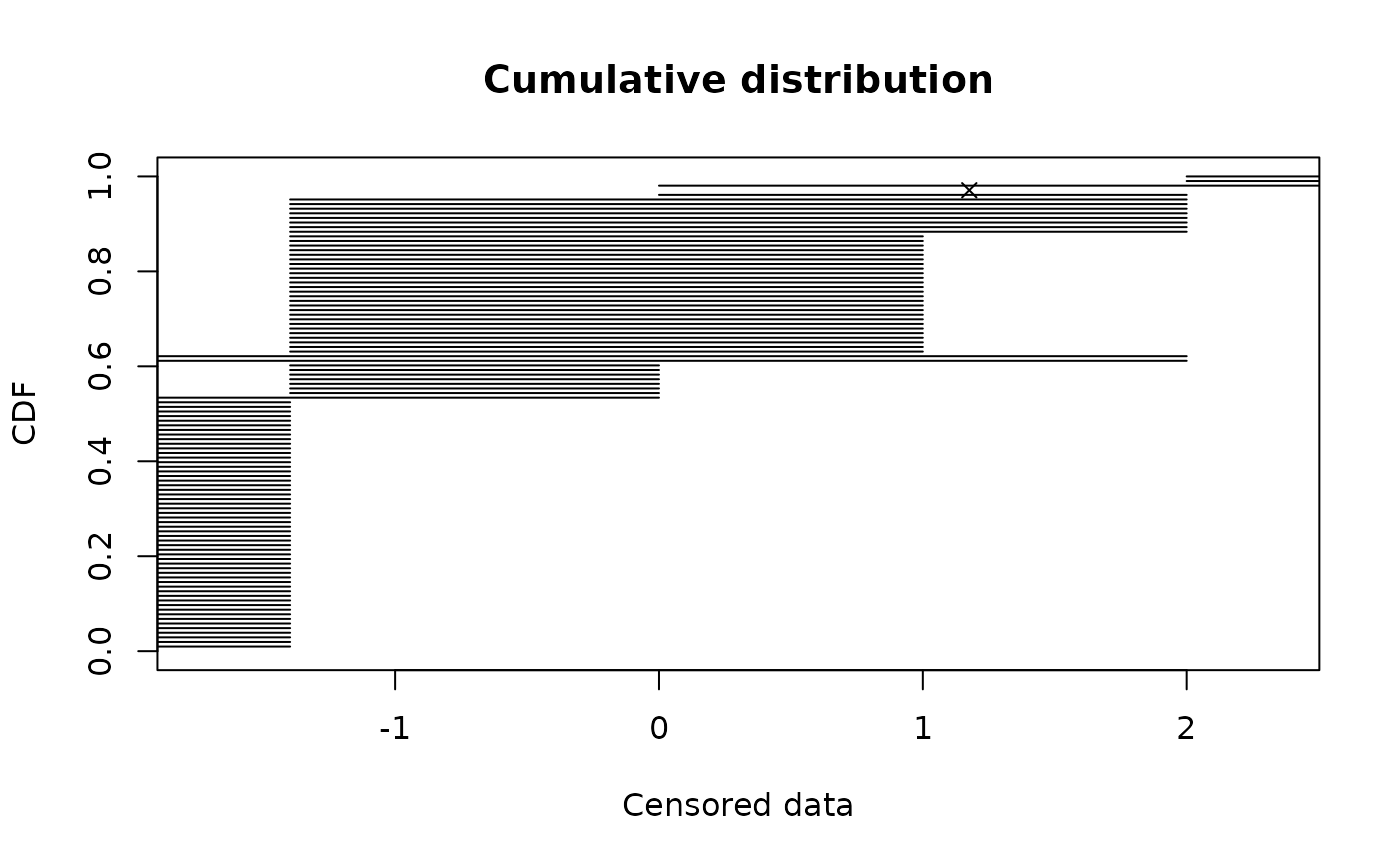
Plot of empirical and theoretical distributions for censored data

Plots an empirical distribution for censored data with a theoretical one if specified.

Usage

plotdistcens(censdata, distr, para, leftNA = -Inf, rightNA = Inf,
    NPMLE = TRUE, Turnbull.confint = FALSE, 
    NPMLE.method = "Wang", ...)

Arguments

censdata: A dataframe of two columns respectively named left and right, describing each observed value as an interval. The left column contains either NA for left censored observations, the left bound of the interval for interval censored observations, or the observed value for non-censored observations. The right column contains either NA for right censored observations, the right bound of the interval for interval censored observations, or the observed value for non-censored observations.
distr: A character string "name" naming a distribution, for which the corresponding density function dname and the corresponding distribution function pname must be defined, or directly the density function.
para: A named list giving the parameters of the named distribution. This argument may be omitted only if distr is omitted.
leftNA: the real value of the left bound of left censored observations : -Inf or a finite value such as 0 for positive data for example.
rightNA: the real value of the right bound of right censored observations : Inf or a finite value such as a realistic maximum value.
NPMLE: if TRUE an NPMLE (nonparametric maximum likelihood estimate) technique is used to estimate the cdf curve of the censored data and previous arguments leftNA and rightNA are not used (see details)
Turnbull.confint: if TRUE confidence intervals will be added to the Turnbull plot. In that case NPMLE.method is forced to "Turnbull.middlepoints"
NPMLE.method: Three NPMLE techniques are provided, "Wang", the default one, rewritten from the package npsurv using function constrOptim from the package stats for optimisation, "Turnbull.middlepoints", an older one which is implemented in the package survival and "Turnbull.intervals" that uses the same Turnbull algorithm from the package survival but associates an interval to each equivalence class instead of the middlepoint of this interval (see details). Only "Wang" and "Turnbull.intervals" enable the derivation of a Q-Q plot and a P-P plot.
...: further graphical arguments passed to other methods. The title of the plot can be modified using the argument main only for the CDF plot.

Details

If NPMLE is TRUE, and NPMLE.method is "Wang" , empirical distributions are plotted in cdf using either the constrained Newton method (Wang, 2008) or the hierarchical constrained Newton method (Wang, 2013) to compute the overall empirical cdf curve. If NPMLE is TRUE, and NPMLE.method is "Turnbull.intervals" , empirical are plotted in cdf using the EM approach of Turnbull (Turnbull, 1974). In those two cases, grey rectangles represent areas where the empirical distribution function is not unique. 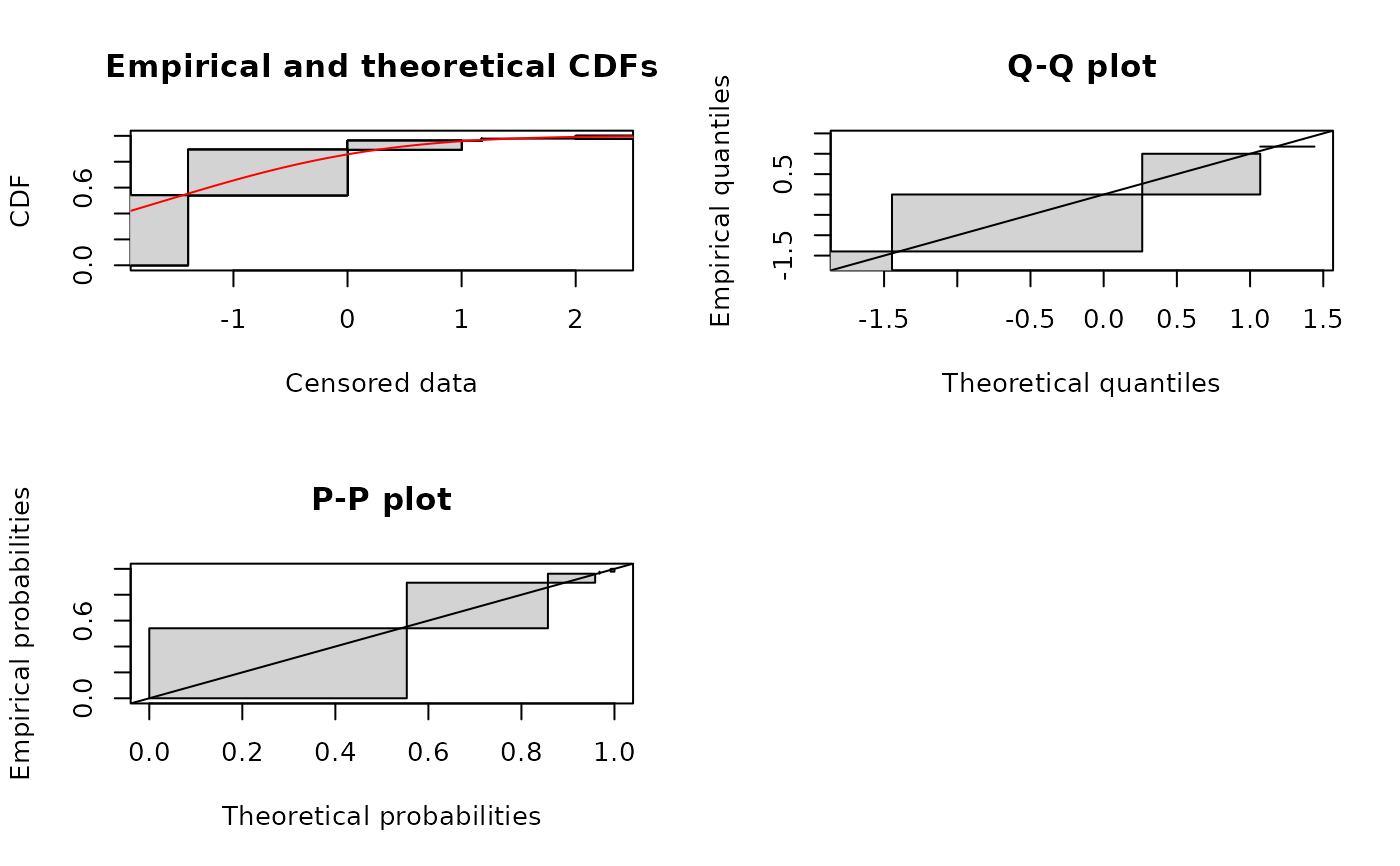In cases where a theoretical distribution is specified, two goodness-of-fit plots are also provided, a Q-Q plot (plot of the quantiles of the theoretical fitted distribution (x-axis) against the empirical quantiles of the data) and a P-P plot (i.e. for each value of the data set, plot of the cumulative density function of the fitted distribution (x-axis) against the empirical cumulative density function (y-axis)). Grey rectangles in a Q-Q plot or a P-P plot also represent areas of non uniqueness of empirical quantiles or probabilities, directly derived from non uniqueness areas of the empirical cumulative distribution.

If NPMLE is TRUE, and NPMLE.method is "Turnbull.middlepoints", empirical and, if specified, theoretical distributions are plotted in cdf using the EM approach of Turnbull (Turnbull, 1974) to compute the overall empirical cdf curve, with confidence intervals if Turnbull.confint is TRUE, by calls to functions survfit and plot.survfit from the survival package.

If NPMLE is FALSE empirical and, if specified, theoretical distributions are plotted in cdf, with data directly reported as segments for interval, left and right censored data, and as points for non-censored data. Before plotting, observations are ordered and a rank r is associated to each of them. Left censored observations are ordered first, by their right bounds. Interval censored and non censored observations are then ordered by their mid-points and, at last, right censored observations are ordered by their left bounds. If leftNA (resp. rightNA) is finite, left censored (resp. right censored) observations are considered as interval censored observations and ordered by mid-points with non-censored and interval censored data. It is sometimes necessary to fix rightNA or leftNA to a realistic extreme value, even if not exactly known, to obtain a reasonable global ranking of observations. After ranking, each of the n observations is plotted as a point (one x-value) or a segment (an interval of possible x-values), with an y-value equal to r/n, r being the rank of each observation in the global ordering previously described. This second method may be interesting but is certainly less rigorous than the other methods that should be prefered.

References

Turnbull BW (1974), Nonparametric estimation of a survivorship function with doubly censored data. Journal of American Statistical Association, 69, 169-173, doi:10.2307/2285518 .

Wang Y (2008), Dimension-reduced nonparametric maximum likelihood computation for interval-censored data. Computational Statistics & Data Analysis, 52, 2388-2402, doi:10.1016/j.csda.2007.10.018 .

Wang Y and Taylor SM (2013), Efficient computation of nonparametric survival functions via a hierarchical mixture formulation. Statistics and Computing, 23, 713-725, doi:10.1007/s11222-012-9341-9 .

Wang, Y., & Fani, S. (2018), Nonparametric maximum likelihood computation of a U-shaped hazard function. Statistics and Computing, 28(1), 187-200, doi:10.1007/s11222-017-9724-z .

Delignette-Muller ML and Dutang C (2015), fitdistrplus: An R Package for Fitting Distributions. Journal of Statistical Software, 64(4), 1-34, doi:10.18637/jss.v064.i04 .

Author

Marie-Laure Delignette-Muller and Christophe Dutang.

Examples

# (1) Plot of an empirical censored distribution (censored data) as a CDF
# using the default Wang method
#
data(smokedfish)
d1 <- as.data.frame(log10(smokedfish))
plotdistcens(d1)


# (2) Add the CDF of a normal distribution 
#
plotdistcens(d1, "norm", para=list(mean = -1.6, sd = 1.5))


# (3) Various plots of the same empirical distribution 
#
# default Wang plot with representation of equivalence classess
plotdistcens(d1, NPMLE = TRUE, NPMLE.method = "Wang")

# same plot but using the Turnbull alorithm from the package survival
plotdistcens(d1, NPMLE = TRUE, NPMLE.method = "Wang")
# Turnbull plot with middlepoints (as in the package survival)
plotdistcens(d1, NPMLE = TRUE, NPMLE.method = "Turnbull.middlepoints")
# Turnbull plot with middlepoints and confidence intervals
plotdistcens(d1, NPMLE = TRUE, NPMLE.method = "Turnbull.middlepoints", Turnbull.confint = TRUE)

# with intervals and points
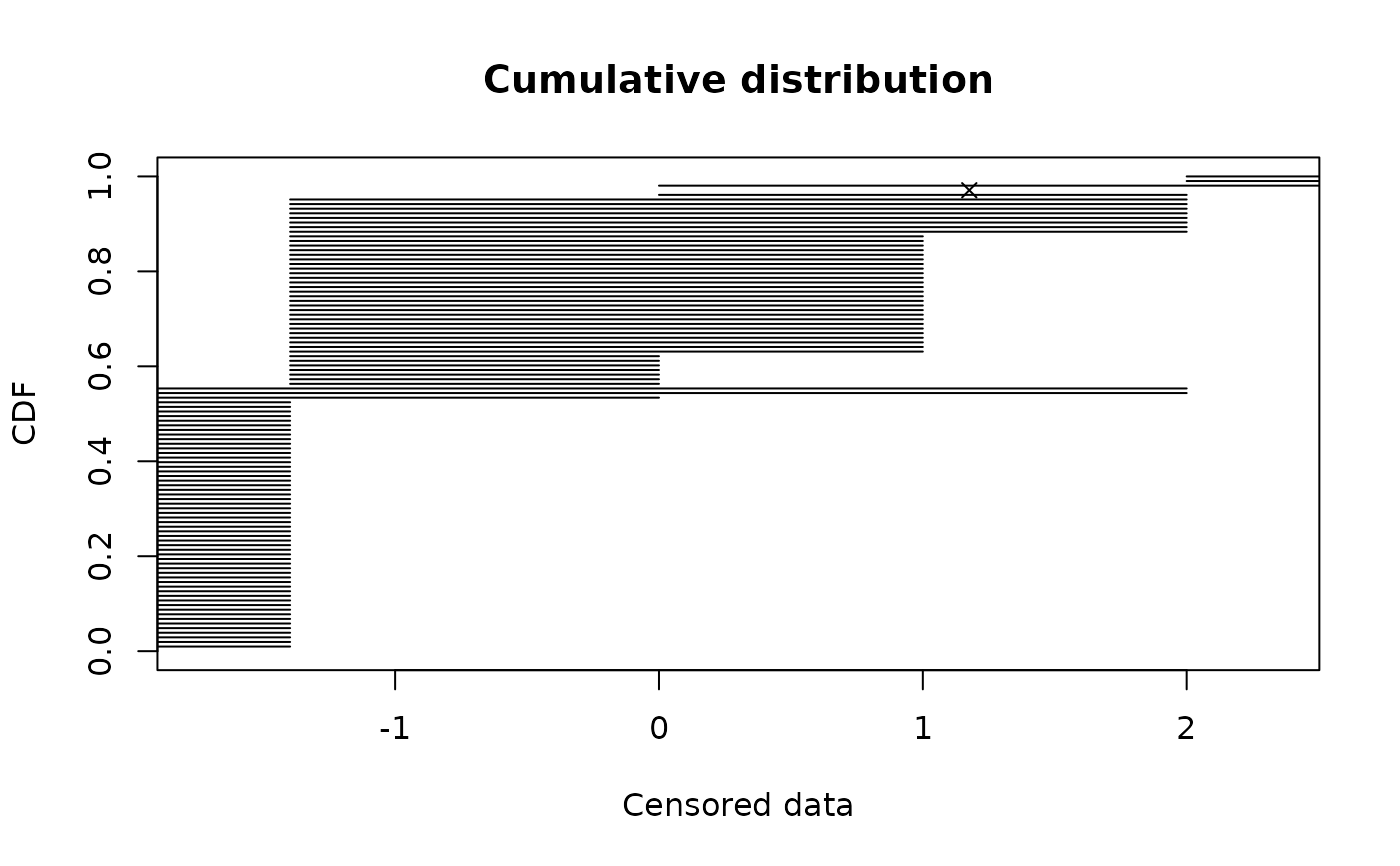
plotdistcens(d1,rightNA=3, NPMLE = FALSE)

# with intervals and points
# defining a minimum value for left censored values
plotdistcens(d1,leftNA=-3, NPMLE = FALSE)